(2) Talking About Chinese Word Segmentation: Trie, KMP, AC Automaton

Trie Tree

In the previous article, we discussed some matching algorithms. However, in addition to algorithms, an efficient data structure is necessary. Storing words in a simple list like [‘中国人’, ‘中东人’] is not practical. Imagine having hundreds of thousands of words—the memory usage of such a list would be enormous.

A Trie tree, also known as a prefix tree, originates from the word retrieval and is pronounced like “try.” Trie trees provide an efficient data structure for word segmentation. Essentially, it is a tree-like structure. For example, a Trie tree constructed from the strings “中国人” and “中东人” would look like the diagram below. It’s clear from the structure that Trie trees effectively save memory space by reusing common prefixes like “中.”

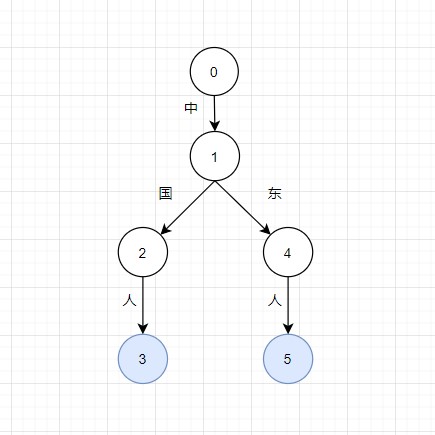
1605767937-1

Moreover, Trie trees optimize query speed. If words are stored in a list with 200,000 entries, the worst-case scenario involves traversing the entire list to find a match, consuming significant computational resources. In contrast, Trie tree queries depend on the length of the search string. For example, querying 中国人 requires at most three lookups.

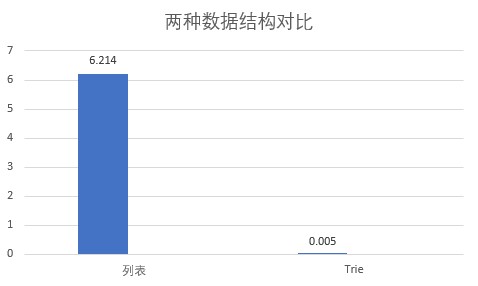
The diagram below shows the runtime of Forward Maximum Matching using a dictionary stored as a list versus a Trie tree. The dictionary contains around 100,000 words, and the text length is 150 characters. The efficiency improvement with the Trie tree is evident.

1605767940-2

Trie trees search for words layer by layer rather than traversing the dictionary directly. For example, to query “中国人”:

Check if the first character, “中,” exists in the first layer.
If “中” exists, move to the next layer and check for “国.”
Repeat the process for “人.” If “人” is found and marked as the end of a word, the query is successful.

To implement such a data structure, the following functions are required:

Word Query: To check if a word exists.
Word Addition: To add new words to the Trie.

Each node represents a character, and a special key, __value, indicates whether a node is the end of a word. The following implementation achieves this:

class Trie:
    def __init__(self):
        self._children = {}
    def _add_word(self, word):
        child = self._children
        for i, char in enumerate(word):
            if char not in child:
                child[char] = {'__value': False}
            if i == (len(word) - 1):
                child[char]['__value'] = True
            child = child[char]
        return True
    def _get_word(self, word):
        child = self._children
        for char in word:
            child = child.get(char)
            if child is None:
                return False
        return child['__value']

After implementing the Trie tree, it can be used to enhance the efficiency of Forward or Backward Matching algorithms. Here is an updated version of the Forward Maximum Matching algorithm using a Trie tree:

trie = Trie()
trie._add_word('分词')

sentence = '中文分词算法' 
start = 0 
maxWidth = 2  # Manually set maximum word length
cut_result = []

while (start <= len(sentence)):
    end = start + maxWidth     
    word = sentence[start: end] 
    while word:
        if trie._get_word(word):
            cut_result.append(word)
            start = start + len(word) - 1  
            break 
        if len(word[:-1]) == 0:
            cut_result.append(word) 
            break
        word = word[:-1]  
    start += 1

print(cut_result)
# ['中', '文', '分词', '算', '法']

KMP Algorithm

With efficient data structures in place, we can take a step further by adopting more advanced search algorithms, such as the AC Automaton. Before diving into the AC Automaton, understanding the KMP algorithm can help in grasping its concepts more easily. Although the AC Automaton can be understood independently, familiarity with the KMP algorithm provides additional clarity.

The KMP algorithm, introduced in 1977 by James H. Morris, Donald Knuth, and Vaughan Pratt, is named after the initials of its inventors. Its core idea is to leverage information from previously matched strings to reduce the number of unnecessary comparisons, thereby improving search efficiency.

Regular Search Example

Let’s first consider a basic search approach to find the position of a substring in a larger text. For instance, take the search word ABABC and the text ABABABC. In a conventional method:

Compare the first character of the search word with the first character of the text.

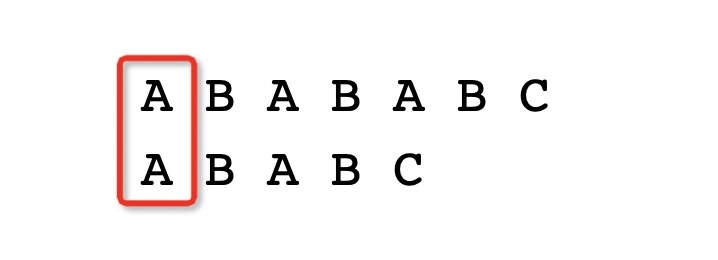
If the characters match, move to the next character and continue comparing.

Continue this process until a mismatch occurs (e.g., the fifth character).

Shift the search word by one position and start over.

Repeat the comparison process until a full match is found. The first occurrence of the search word is at position 3.

Inefficiency in Regular Search

In the above example, the second search attempt results in redundant comparisons. For large-scale text searches, such inefficiencies accumulate and lead to unnecessary computational costs. The KMP algorithm addresses this by minimizing invalid matches, thereby improving efficiency.

Partial Match Table

A key component of the KMP algorithm is the Partial Match Table (or Failure Function), which is a table of non-negative integers corresponding to each character of the search word. It helps determine the next position to start matching after a mismatch.

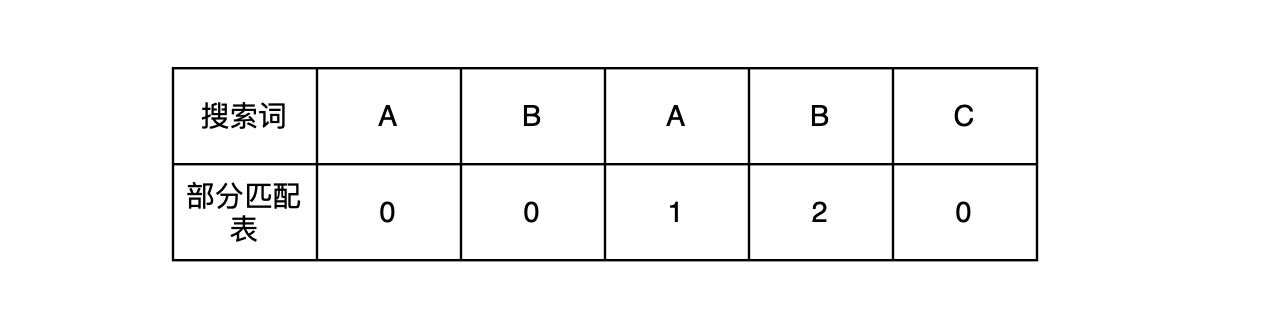
For example, the partial match table for ABABC is:

To use this table, let’s revisit the example:

Begin the first comparison.

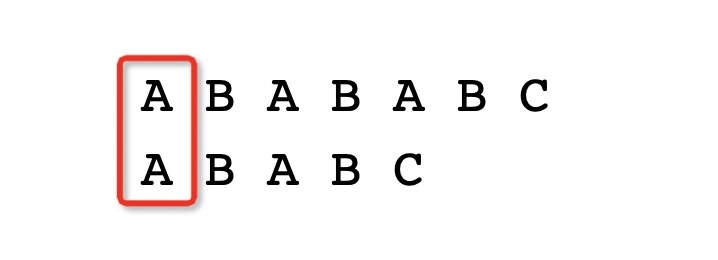
Successfully match the first four characters.

On the fifth character, a mismatch occurs (C vs. A). The partial match table now determines the next starting position, skipping redundant comparisons. The formula used is:

Shift Value = Number of Matched Characters - Value in Partial Match Table for the Previous Character

For instance, at the fifth character, the table value for the previous character is 2. With 4 matched characters, the next starting position is shifted by 4 - 2 = 2.

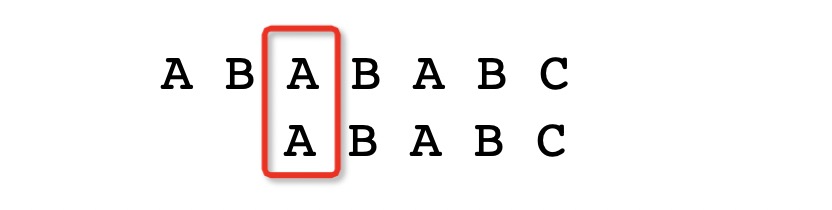
This skips the second comparison, significantly improving efficiency for large-scale searches.

Calculating the Partial Match Table

The values in the partial match table represent the length of the longest matching prefix and suffix for each position in the search word. To calculate these values:

Prefixes: All initial segments of a string, excluding the entire string.
Suffixes: All terminal segments of a string, excluding the entire string.

For example, for the word home:

Prefixes: {h, ho, hom}
Suffixes: {ome, me, e}

For ABABC, the partial match table is calculated as follows:

A: Prefix and suffix are empty → Value = 0
AB: Prefix {A}, Suffix {B} → No match → Value = 0
ABA: Prefix {A, AB}, Suffix {BA, A} → Match "A" → Value = 1
ABAB: Prefix {A, AB, ABA}, Suffix {BAB, AB, B} → Match "AB" → Value = 2
ABABC: Prefix {A, AB, ABA, ABAB}, Suffix {BABC, ABC, BC, C} → No match → Value = 0

This table allows the KMP algorithm to efficiently jump over redundant comparisons, making it highly effective for large-scale text searches.

AC自动机

AC自动机(Aho-Corasick automaton)是一种基于Trie树进行匹配的一种字符串搜索算法，在1975年由Alfred V. Aho和Margaret J.Corasick发明，该算法其实和KMP算法并无太大的关联，KMP算法是1对1（一个搜索词匹配一个文本）进行搜索，而AC自动机则是1对多（多个搜索词匹配一个文本）进行搜索。 AC自动机对比Trie树的优点在于Trie树每次匹配后进行下一个字符查找的时候都需要回到顶点继续再搜索，而AC自动机则是将该文本中的字符串搜索一次性完成。 AC自动机核心是利用一个叫fail指针(失败指针)的东西，fail指针主要的用途是如果当前字符在当前节点的子元素中没有找到，那么就利用fail指针指向另外一个节点继续搜索，直到搜索完成，下图中的红线就是一个fail指针。

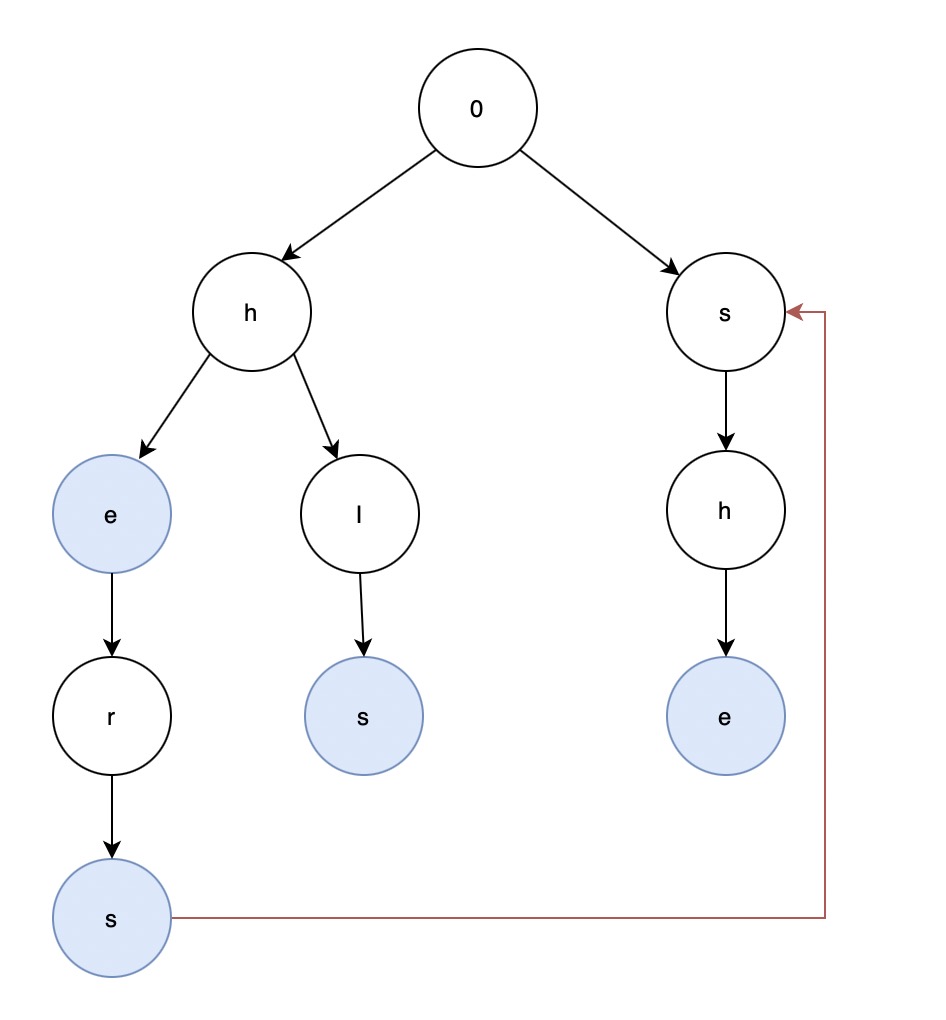
比如单词列表为['he', 'hers', 'his', 'she']，待分词文本为hershe，正常Trie匹配为先找到he，然后字符r再从0开始匹配，此时r没有在顶层节点的子节点当中，所以跳过，继续查找，直到找到了she完成。而AC自动机的算法则为当找到了he单词后，继续在当前节点的子节点当中搜索字符r，如果有继续搜索下一个字符s，然后得到单词信息hers，然后继续搜索字符h，此时搜索位置为下图红色节点位置，但该节点下没有h：

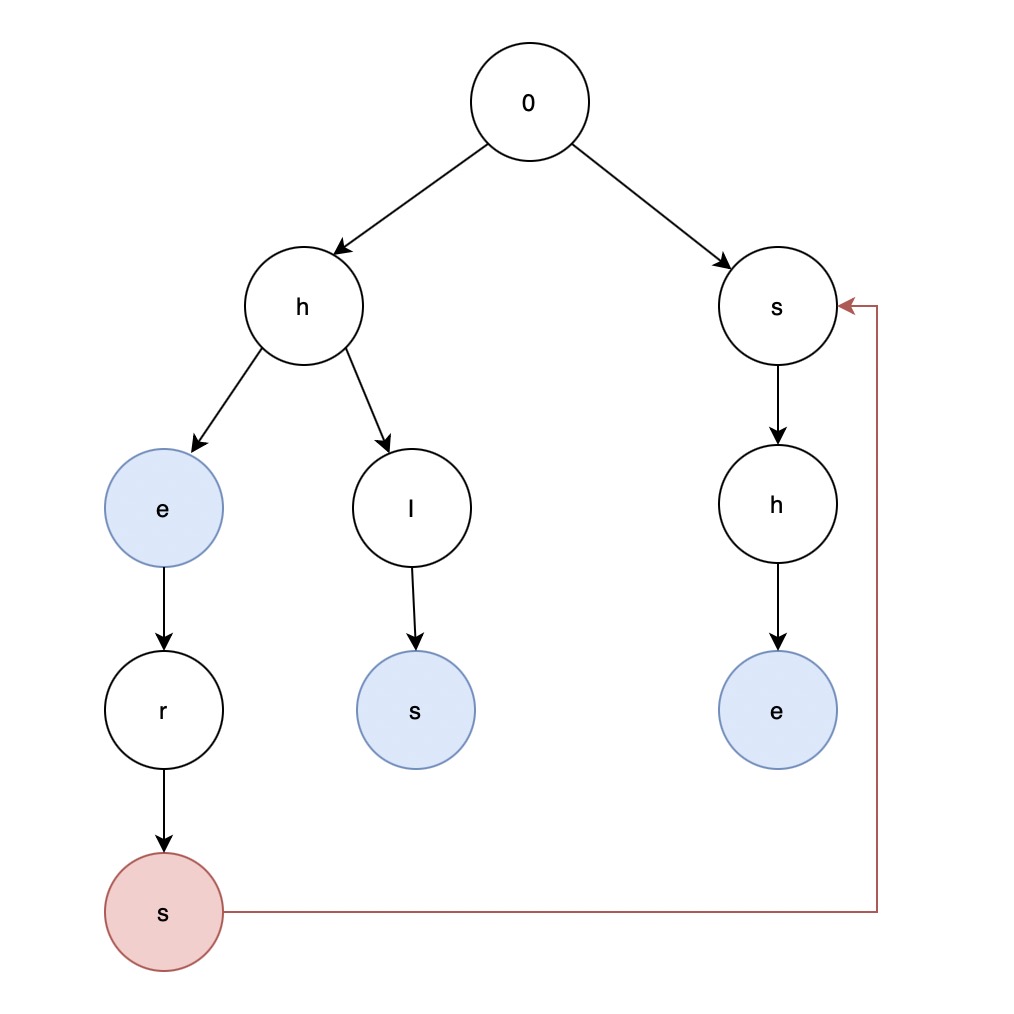
这个时候就查看当前节点（即红色节点）的fail指针(红线)指向的节点下是否有字符h，此时发现有，则通过fail指针继续查找，直到找到了单词she。 AC自动机的理念是比较好理解，而难点在于如何计算fail指针指向谁，计算fail指针可以通过BFS（层次遍历），BFS将Trie每一层进行遍历，遍历的时候将计算所有子节点的fail指针，并将子节点放入到一个先进先出容器当中（队列）便于访问子节点的子节点。而计算fail指针的时候一定是当前字符不存在于当前节点的子节点当中，所以查找当前节点的子节点的fail指针的时候，可以通过将当前节点的子节点中的所有fail指针都可以获取到所有父节点的fail指针，然后一层一层的找，如果找到后就指向谁，如果没有找到则指向最顶层。下面是实现的代码：

class TrieNode(object):
    def __init__(self) -> None:
        self._children = {}
        self._fail = None
        self._exist = []
    def _add_child(self, char, value, overwrite = None):
        child = self._children.get(char)
        if child is None:
            child = TrieNode()
            self._children[char] = child
        if overwrite:
            child._exist.append(value)
        return child

class Trie(TrieNode):
    def __init__(self) -> None:
        super().__init__()
    def _find_text(self, text):
        state = self
        cut_word = []
        for i,t in enumerate(text):
            while state._children.get(t) is None and state._fail:
                state = state._fail
            if state._children.get(t) is None:
                continue
            state = state._children.get(t)
            if len(state._exist) != 0:
                for x in state._exist:
                    max_cut = text[i - x + 1:i + 1]
                    cut_word.append(max_cut)
        return cut_word
    def __setitem__(self, key, value):
        state = self
        for char in key:
            if char == key[-1] :
                state = state._add_child(char, len(value), True)
                break
            state = state._add_child(char, None, False)
    def _init_fail(self):
        q = queue.Queue()
        for i in self._children:
            state = self._children.get(i)
            state._fail = self
            q.put(state)
        while q.empty() == False:
            state = q.get()
            for i in state._children:
                v = state._children.get(i)
                fafail = state._fail
                while fafail is not None and fafail._children.get(i) is not None:
                    fafail = fafail._children.get(i)
                v._fail = fafail
                if v._fail:
                    if len(fafail._exist) != 0:
                        v._exist.extend(v._fail._exist)
                q.put(v)

AC Automaton

The AC Automaton (Aho-Corasick automaton) is a string matching algorithm based on the Trie tree. It was invented in 1975 by Alfred V. Aho and Margaret J. Corasick. Unlike the KMP algorithm, which performs one-to-one (single pattern to single text) matching, the AC Automaton handles one-to-many (multiple patterns to single text) matching.

Compared to Trie trees, the AC Automaton has a significant advantage. In a Trie tree, after each match, the search must return to the root node to continue. The AC Automaton, however, can complete the entire string search in one pass. The core of the AC Automaton is the fail pointer, which ensures that if a character cannot be found in the current node’s children, the fail pointer directs the search to another node. The fail pointer is represented by red lines in the diagram below.

Example

Consider the word list ['he', 'hers', 'his', 'she'] and the text hershe. Using a standard Trie tree, the process would:

Match he, then return to the root to search for r.
Continue until she is matched.

In contrast, the AC Automaton:

Matches he, continues to search r in the current node’s children, then finds hers.
Continues with h. At this point, the node lacks h as a child:

The fail pointer redirects the search to a node where h exists, enabling the algorithm to locate she.

Fail Pointer Calculation

The concept of the AC Automaton is relatively straightforward; the challenge lies in calculating the fail pointers. This is done using Breadth-First Search (BFS), where each level of the Trie is traversed. During traversal, fail pointers are calculated for all child nodes, and these child nodes are added to a queue (FIFO) for further processing.

When calculating a fail pointer:

If the current character is not found in the current node’s children, check the parent node’s fail pointer for the same character.
Repeat this process until a match is found or the root node is reached.

Implementation

Below is a Python implementation of the AC Automaton:

class TrieNode(object):
    def __init__(self) -> None:
        self._children = {}
        self._fail = None
        self._exist = []
    def _add_child(self, char, value, overwrite=None):
        child = self._children.get(char)
        if child is None:
            child = TrieNode()
            self._children[char] = child
        if overwrite:
            child._exist.append(value)
        return child

class Trie(TrieNode):
    def __init__(self) -> None:
        super().__init__()
    def _find_text(self, text):
        state = self
        cut_word = []
        for i, t in enumerate(text):
            while state._children.get(t) is None and state._fail:
                state = state._fail
            if state._children.get(t) is None:
                continue
            state = state._children.get(t)
            if len(state._exist) != 0:
                for x in state._exist:
                    max_cut = text[i - x + 1:i + 1]
                    cut_word.append(max_cut)
        return cut_word
    def __setitem__(self, key, value):
        state = self
        for char in key:
            if char == key[-1]:
                state = state._add_child(char, len(value), True)
                break
            state = state._add_child(char, None, False)
    def _init_fail(self):
        q = queue.Queue()
        for i in self._children:
            state = self._children.get(i)
            state._fail = self
            q.put(state)
        while not q.empty():
            state = q.get()
            for i in state._children:
                v = state._children.get(i)
                fafail = state._fail
                while fafail is not None and fafail._children.get(i) is None:
                    fafail = fafail._fail
                v._fail = fafail
                if v._fail:
                    if len(fafail._exist) != 0:
                        v._exist.extend(v._fail._exist)
                q.put(v)

References

(完)

Lucas Wu