线性回归
简单线性回归
线性回归是用来找到两个变量之间关系的方法,它试图找到一个“最佳线路”(即拟合),表示当自变量变化的时候,因变量如何变化,线性回归的公式为如下: $$ y = a \cdot x + b $$ 其变量的解释为:
- y:因变量,也是输出或者预测值。
- x:自变量,也是输入。
- a:为斜率,表示x自变量每增加1,y会增加或者减少多少。
- b:为截距,表示当x=0的时候,y的值。
线性回归可以简单理解为找到一条最能反应数据点总体趋势的数学表达式(比如直线),比如在散点图中,画一条尽可能靠近所有点的直线,而在这条线中,截距b表示直线在y轴上的起点,在当x增加时,直线沿着斜率a的方向延长,延长后的值即为y值。
举一个生活中的例子,通过距离长短(自变量,即x)预测时间(因变量, 即y)的时长:
| 送货距离(km) | 送货时间(min) |
|---|---|
| 1 | 10 |
| 2 | 15 |
| 3 | 20 |
| 4 | 25 |
| 5 | 35 |
通过上述的数据,可以知道当送货距离每增加1公里的时候,送货时间增加5分钟,所以在送货距离为2的时候,公式为: $$ 15 = a \cdot 2 + b $$ 计算斜率a有很多方法,具体取决于解决的问题背景、数据特性等,这里采用简单的“平均变化法”来计算斜率a,“平均变化法”的思路就是选择数据中任意的两个点来估算斜率a,公式为: $$ a = \frac{\Delta y}{\Delta x_1} $$ 举例的数据中,取抽取第一个点和最后一个点来计算斜率a为(不一定要用最后一个点和第一个点,取具备代表的两个点即可): $$ (35 - 10) / (5 - 1) = 6.25 $$ 这个时候将斜率带入线性回归的公式中: $$ 15 = 6.25 \cdot 2 + b $$ 然后通过公式计算出截率b为2.5,因此公式为: $$ b = y - a \cdot x \newline b = 15 - 6.25 \cdot 2 = 2.5 $$ 最后我们就得到了一个预测模型,当我们输入x的时候,就会预测出y的值: $$ y = 6.25 \cdot x + 2.5 $$ 通过这个模型可以进行计算当距离达到了3KM的时候,预测出来的送货时间为21.25分钟: $$ 6.25 \cdot 3 + 2.5 = 21.25 $$ 需要注意的是模型并不会精准的预测出在上述数据表中对应的值,因为拟合的直线是代表的整体的趋势,在实际的数据中拟合的直线也不会穿过每个数据点,所以更多的时候是考虑了所有数据点的情况去拟合一条合适的直线,所以预测的是有偏差的。
多元线性回归
线性回归是用一条直线来描述两个变量之间的关系,而多元线性回归则是用一个公式来描述多个自变量对一个因变量的共同影响,其公式为: $$ y = a_1 \cdot x_1 + a_2 \cdot x_2 + a_3 \cdot x_3 + … + b $$
- y:为因变量,即预测变量或目标变量。
- x_1至x_n:为自变量,即影响目标变量的因素。
- a_1至a_n:为每个自变量对应的斜率(影响系数)。
- b:为截距,即当所有的x为0的时候,y的值。
多元线性回归和线性回归公式理解上是差不多的难度,因为变动部分只增加了不同的x和a,比如还是拿外卖的例子来距离,并且在原有基础上增加订单数量对送货时间的影响:
| 送货距离(km) | 订单数量 | 送货时间(min) |
|---|---|---|
| 1 | 1 | 15 |
| 2 | 2 | 25 |
| 3 | 1 | 30 |
| 4 | 3 | 40 |
| 5 | 1 | 45 |
还是通过平均变化法来计算每个自变量的斜率(或者称为影响系数): $$ a1 = (45 - 15) / (5 - 1) = 7.5 \newline a2 = (40 - 25) / (3 - 2) = 15 $$ 然后再通过平均的方式计算截距b,因为截距b是代表是当所有x为0的时候y的值,所以截距b是一个全局参数,它应该反应的是所有数据点的整体趋势,避免需要某一个点计算截距导致的放大随机误差或异常点的影响。 $$ x1平均值 = (1 + 2 + 3 + 4 + 5) / 5 = 3 \newline x1平均值 = (1 + 2 + 1 + 3 + 1) / 5 = 1.6 \newline y平均值 = (15 + 25 + 30 + 40 + 45) / 5 = 31 $$ 然后带入公式计算截距: $$ b = \overline{y} - a_1 \cdot \overline{x}_1 - a_2 \cdot \overline{x}_2 \newline b = 31 - 3 * 7.5 - 1.6 * 15 = -15.5 $$ 最后得到预测公式: $$ y = x1 \cdot 7.5 + x2 \cdot 15 + -15.5 $$ 然后利用上面的公式进行预测当送货距离为4,订单数量为3的时候,预测的y值为31.44: $$ 4 \cdot 7.5 + 3 * 15 + -15.5 = 59.5 $$
线性回归评估
线性模型常用两种方式进行可视化的评估,第一种是Residual Plot(残差图),第二种是Distribution Plot(分布图)。
Residual Plot
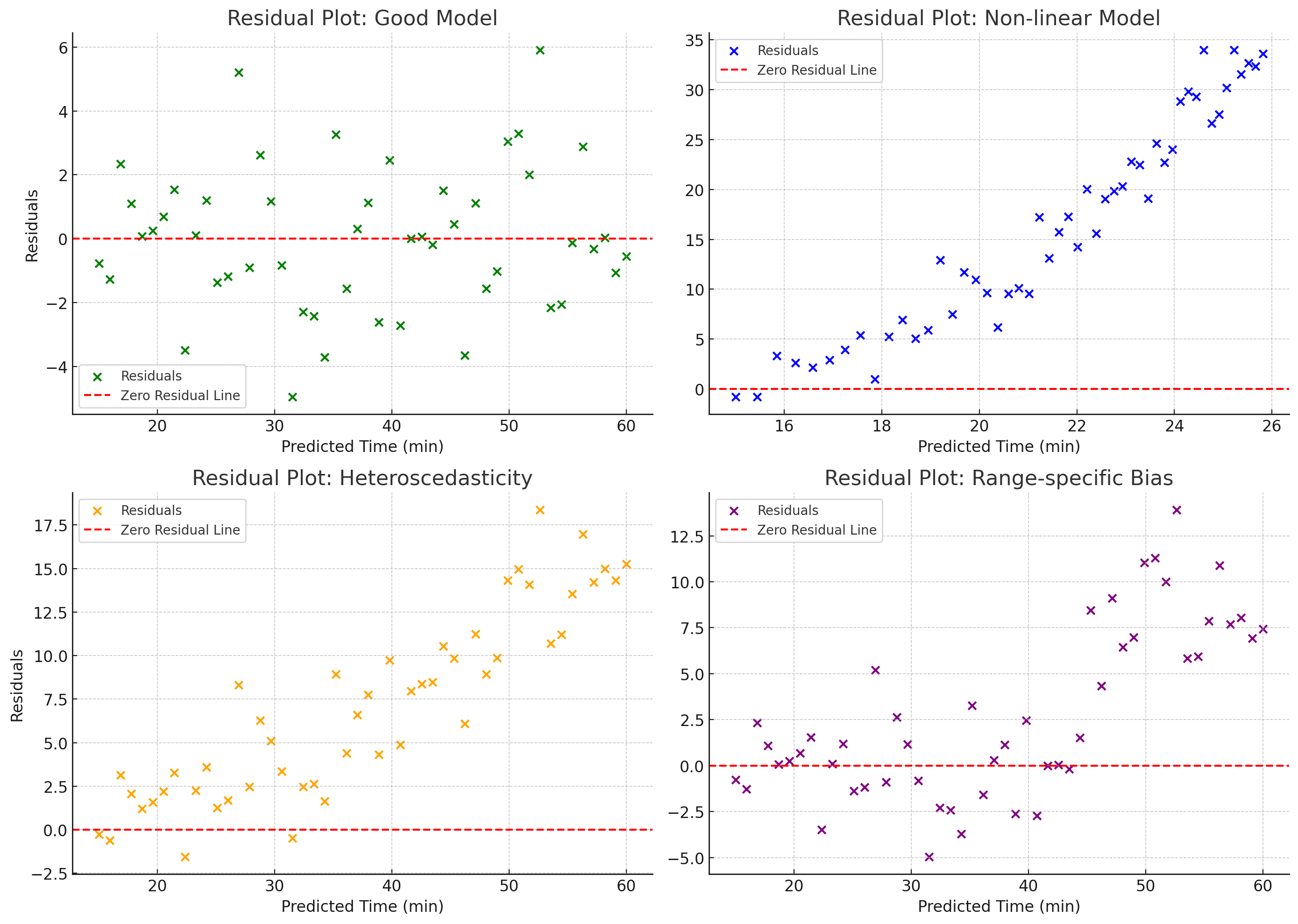
残差图的原理是实际值和预测值的差值(残差)与预测值的关系,通过残差图可以得知如下的三点:
- 是否满足线性关系:残差应该是随机分布零线的上下,没有明显的趋势,如果出现曲线趋势,说明不具备线性关系,线性回归模型不适合。
- 是否均匀分布,预测是不是偏向某些范围:残差应该随机分布在0的上下,且没有锥形等不均匀模式(即误差随预测值增大而增大或者减小),如果存在锥形说明模型对于某些范围的预测误差较大。
- 是否有异常极端值(离群点):如果出现了极端的离群点,说明存在异常值,可能会对模型产生不良的影响。
而残差值能够告诉我们:
- 正残差:说明预测值比实际值小,存在低估可能
- 负残差:说明预测值比实际值大,存在高估可能
- 残差为零:说明预测值和实际值完全一样
比如下图中四种不同的情况,第一种良好模型,第二种为非线性模型,第三种为分布不均匀模型,第四种为部分偏差图形(即右侧部分会存在对数据的低估可能)。
Distribution Plot
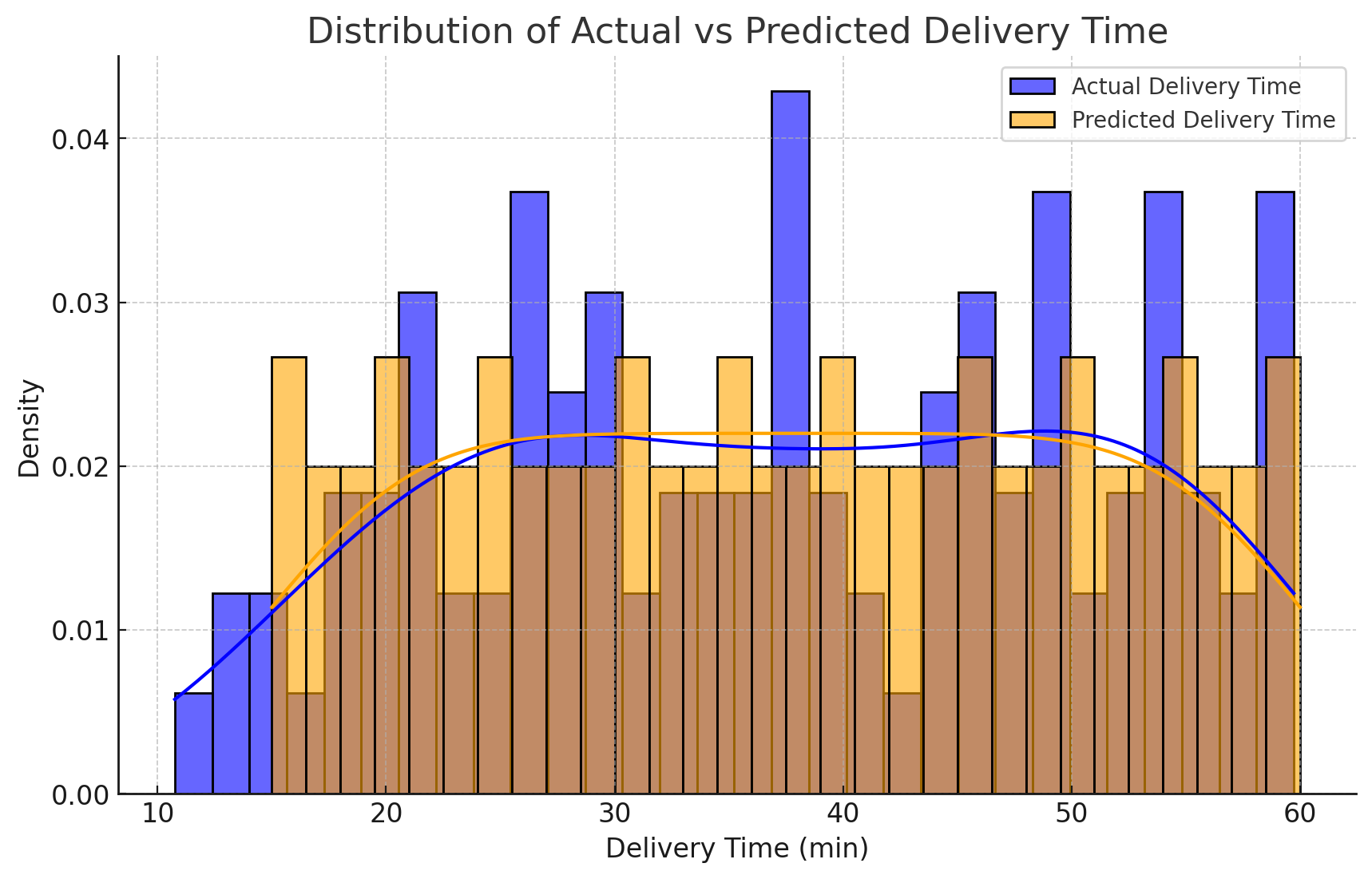
分布图是用来展示一组数据概率密度分布,即数据在不同取值范围的分布情况,横轴是数据的取值(例如实际值或预测值),纵轴是每个取值范围内的频率或者密度,根据绘制预测值和实际值的分布图,能清楚的看见预测值和实际值的重叠情况。
比如下面的分布图,蓝色为实际值,橙色为预测值,深橙色为重叠部分,除此之外可以通过曲线进行观察,蓝色的曲线更宽,说明范围更大,可能包含了其它的随机因素(比如外卖的天气、交通等),橙色更短,说明模型的预测值较为集中,忽略了一部分数据的随机性。
绘图
在Python中,Residual Plot图可以采用Seaborn中的rediplot绘制,而Distribution Plot则可以采用Seaborn中的displot绘制。
(完)