(二)漫话中文分词:Trie、KMP、AC自动机
Trie树
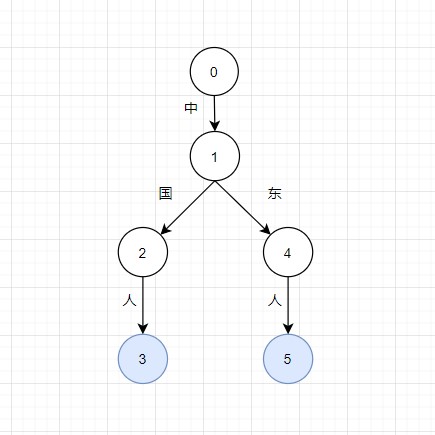
在上一篇文章当中,说到了一些匹配的算法,但是算法有了,还得需要一个高效的数据结构,不能只是通过[‘中国人’, ‘中东人’]等结构来进行存放,可以想象一下,如果有几十万的词,那么这个列表的占用的内存非常大。 Trie树,也被称为前缀树,该词源自单词retrieval,发音和try相同,Trie树可为词库提供一种高效的分词数据结构,该结构本质上是一种树状数据结构,比如"中国人"、“中东人"三个字符串构造的Trie树为下图,图中能够很清楚的看见,Trie树结构能够很好的节省相同前缀单词所浪费的空间,因为这两个词都是以"中"开头,所以可以使用同一个父辈节点。
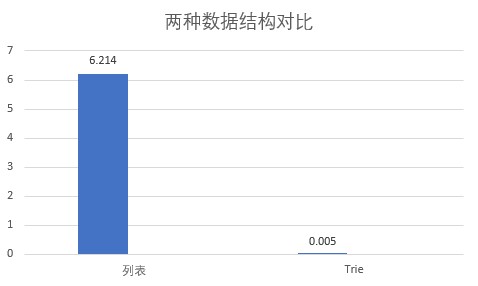
除此之外,Trie树还对查询的速度有一定的优化,如果以列表存放词来说,如果列表存放的词达到了20万个,那么最坏的情况是你需要匹配的词在存放于列表最后,那么就相当于要将这20万个词全部遍历,可想而知浪费了非常多的计算资源。 而Trie查询的次数最大的次数取决于查找的字符串长度,比如中国人,那么查询次数最大仅为3次。 下图为基于同一份10万左右的词典,待分词文本为字符长度150,使用正向最大匹配算法在列表和Trie两种结构上进行分词的运行时间,从下图可以看出来差距非常大。
Trie树的查找方式则是通过层层查询,而不是直接遍历词典,比如"中国人”,首先会查找第一层中是否有"中"这个字符,如果没有查询到则返回查询失败,如果有则继续查找"中"字符对应的下一层是否有"国",如果没有则返回查询识别,如果有则继续查找"国"下一层是否有"人",此时找到存在"人"这个节点,并且该节点标注为蓝色,表明是一个词,所以返回该字符串为一个词。 其实要实现这样的数据结构,大致的功能点为下面两点:
- 查询词
- 添加词
除此之外还需要考虑如果标记词的结束节点,首先可以约定,默认情况都返回"False"表示为未查询到或设置失败,而返回"True"则表示查询到或设置成功,每个节点为一个字符,而字典当中的__value表示是否为结束节点(即一个词的尾字符),如果是则为True,不是则为False,整体可以采用函数或者类来定义。 实现代码:
class Trie(): #定义一个Trie类型
def __init__(self): #为这个生成的实例定义一个名为_children的对象,用于存放词的Trie结构
self._children = {}
def _add_word(self, word): # 定义一个添加词的实例方法
child = self._children # 首先会将_children的对象赋值给child
for i,char in enumerate(word): # 然后从头遍历添加词的每一个字符
if char not in child: # 查看当前字符是否存在Trie树上
child[char] = {'__value': False} # 如果没有则新建一个对象,并设置特殊key__value为False,表明这不是一个结尾字符
if i == (len(word) - 1): # 判断是否为结尾字符
child[char]['__value'] = True # 如果是则将特殊key:__value设为True,表明为结尾字符
child = child[char] # 如果还有字符,则将当前字符对象更新为child,那么下一次查找则是基于上一次对象下
return True # 添加完成返回True
def _get_word(self, word): # 查找词
child = self._children # 同样设置一个child变量,用于控制当前的字符对象
for char in word:
child = child.get(char)
if child is None : # 只要其中一个没有查找到,那么说明匹配识别,则返回False
return False
return child['__value'] # 如果没有匹配失败则返回特殊__value的值
#回True表示词典中存在该词,返回False表示不存在或者传递进来的词不成词
将Trie实现后,就可以在正向或者反向等算法中来进行使用,从而提高运算的效率,但是使用Trie树的时候,可能无法动态的计算其词的长度,所以根据上一篇文章当中修改的最大正向匹配算法的长度计算我手动计算填写。 下面的代码是基于《[一]漫话中文分词:最大匹配,双向最大,最小词数》文章中的最大正向匹配算法,但其中的词典则是使用Trie结构,改动了两处:
trie = Trie()
trie._add_word('分词')
sentence = '中文分词算法'
start = 0
maxWidth = 2 # 改动1:手动填写最大长度
cut_result = []
while (start <= len(sentence)):
end = start + maxWidth
word = sentence[start: end]
while ( word ) :
if ( trie._get_word(word) ) : # 改动2:利用Trie的查询函数,该返回查询到为词则返回True,否则False
cut_result.append(word)
start = start + len(word) - 1
break
if (len(word[:-1]) == 0):
cut_result.append(word)
break
word = word[:-1]
start = start + 1
print(cut_result)
#['中', '文', '分词', '算', '法']
KMP算法
高效的数据结构有了,然而还可以更近一步,在Trie结构的基础上采用一些高效的查询算法,比如下面的AC自动机,在了解AC自动机之前,可以先了解一下KMP算法,虽然了解AC自动机不需要了解KMP算法就可以理解,但是理解了KMP算法过后,实际上会更容易理解AC自动机。 KMP算法于1977年由James H. Morris](https://en.wikipedia.org/wiki/James_H._Morris)、Donald Knuth、Vaughan Pratt三位发明者联合发表,其算法名称KMP是由三位发明者首字母命名。 KMP算法其核心主要为利用已匹配字符串中的已知信息来减少无效匹配的次数,从而提升查找的效率。首先可以来看看普通查找方式,找到一个字符串在另外一个字符串中出现的位置该怎么来匹配。 比如搜索词ABABC,需要查找在文本ABABABC中出现的位置,那么按照常规的方式应该首先第一个字符,是否相等:
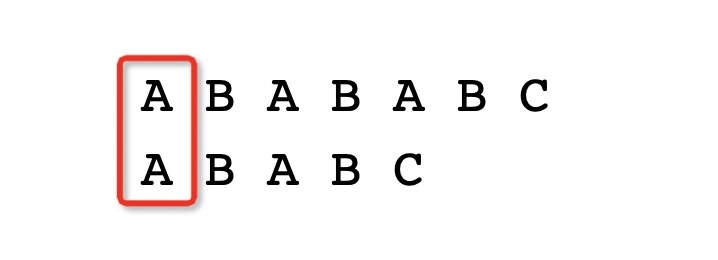
如果第一个字符相等,那么继续匹配第二个字符,查看第二个字符是否相等:

如果第二字符相等再匹配下一个字符是否相等,一直匹配,直到第五个字符出现了问题,不相等:

此时,将搜索词的位置往后移动一位,即搜索词的第一个字符从文本的第二个字符开始匹配:

移动过后,第一位不匹配,那么继续将模式串移动一位,将模式串第一个字符对准字符串第三个字符,继续重新匹配,第一次匹配:
 第一次匹配成功,继续第二位,第三位匹配,一直遍历匹配到搜索词最后一个字符成功,那么整个搜索结束,并返回该搜索词第一次出现的位置为文本的第三位。
第一次匹配成功,继续第二位,第三位匹配,一直遍历匹配到搜索词最后一个字符成功,那么整个搜索结束,并返回该搜索词第一次出现的位置为文本的第三位。

从上面的例子来看,第二次明显属于无效匹配,如果在大量的文本中搜索词的话,会造成更多这样的无效匹配出现,而KMP算法就是解决这样的问题,用来减少无效的匹配次数,从而来增加匹配的效率。 KMP算法首先需要维护一个特殊的表,名字为部分匹配表或者失配函数,这个表由非负数数值构成,并且搜索词的字符都会对应一个数值,大概为下面这样:
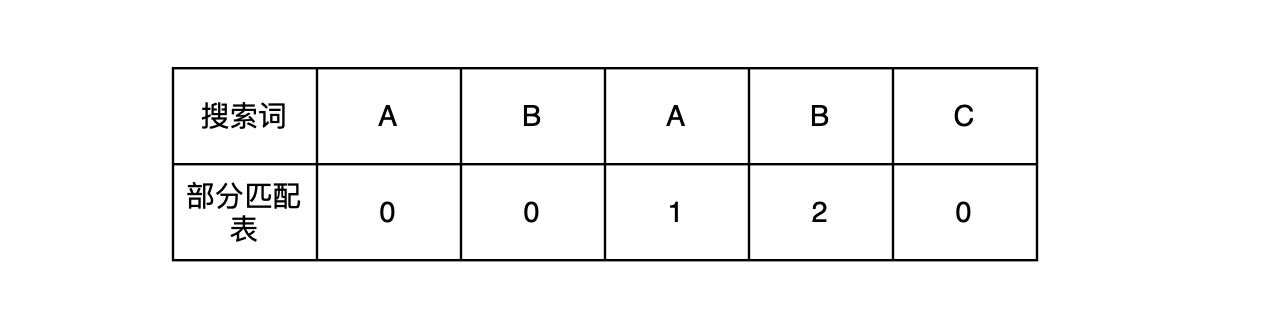
关于这个值是如何计算的先不用管,先看看如何使用这个值来跳过无效的匹配,还是拿刚刚例子,搜索词ABABC,文本ABABABC,首先进行第一次匹配:
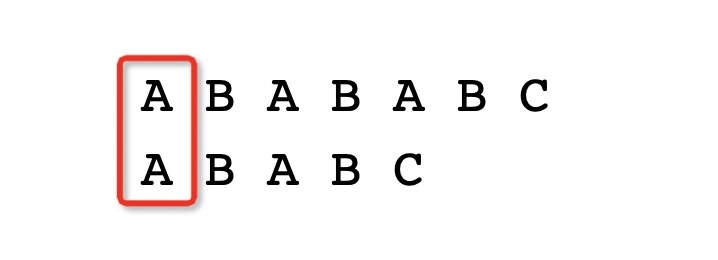
第一次匹配成功,进入第二次匹配:

第二次匹配成功,重复该动作,直到匹配到第五次出现了问题,此时搜索词第五位的C和文本的第五位A不相等,此时KMP算法中的部分匹配表就派上了用场,可以通过该表计算出需要搜索词下一个开始匹配的位置是从什么地方开始,这样就可以跳过无效匹配位的值。其计算公式为:
位移值 = 成功匹配的数量 - 匹配失败位前一位在部分匹配表中的值
因为匹配失败的位置是在第五位,那么获取部分匹配表中的值应该位前一位的值,通过查询下图得到数值2,然后匹配成功的字符数量为4,最后相减得到2。

从上面得到数值后,就可以将搜索词当前开始的位置加2,因为此时的搜索词开始的位置是文本的第1位,那么加上后得到3,就意味着搜索词的第一位对应着文本的第三位:
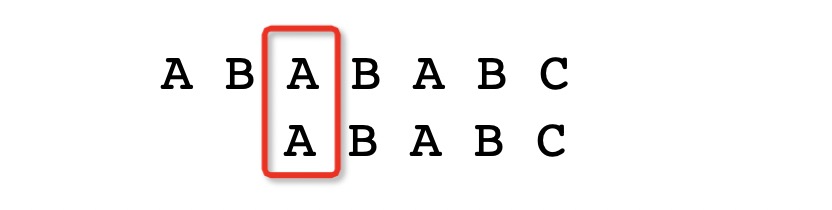
而通过KMP的算法就可以跳过对应普通查找方法的第二次匹配,这在大量的文本搜索当中提升是非常显著的,但是怎么来计算部分匹配表的中的值? 部分匹配表指的是最长相同字符的长度,要计算部分匹配表首先需要知道前缀和后缀的概念,前缀指的是除了字符串第一个字符之外的所有字符串头部集合,而后缀指的是除了字符串最后一个字符之外的所有后部集合。 比如说单词home,其前后缀集合为:
前缀集合为:{h, ho, hom}
后缀集合为:{ome, me, e}
而部分匹配表需要对每一位进行计算相应的值,而在搜索词的每一位取的范围字符为前面所有字符,比如ABABC,计算第一位因为前面没有字符,所以取的范围仅为A。到第二位则包含前面所有字符,所以等于AB。第三位则为ABA以此类推 再回到上面例子中,搜索词ABABC,其计算部分匹配表的过程为:
A:前后缀都为空,则值为0
AB:前缀为{A},后缀为{B},没有相同的字符,部分匹配表中的值为0
ABA:前缀为{A, AB},后缀为{BA, A},其中有字符A交集,其长度为1,部分匹配表中的值为1
ABAB:前缀为{A,AB,ABA},后缀为{BAB,AB,B},有相同字符AB,长度为2,部分匹配表中的值为2
ABABC:前缀为{A,AB,ABA,ABAB},后缀为{BABC,ABC,BC,C},没有相同字符,部分匹配表中的值为0
AC自动机
AC自动机(Aho-Corasick automaton)是一种基于Trie树进行匹配的一种字符串搜索算法,在1975年由Alfred V. Aho和Margaret J.Corasick发明,该算法其实和KMP算法并无太大的关联,KMP算法是1对1(一个搜索词匹配一个文本)进行搜索,而AC自动机则是1对多(多个搜索词匹配一个文本)进行搜索。 AC自动机对比Trie树的优点在于Trie树每次匹配后进行下一个字符查找的时候都需要回到顶点继续再搜索,而AC自动机则是将该文本中的字符串搜索一次性完成。 AC自动机核心是利用一个叫fail指针(失败指针)的东西,fail指针主要的用途是如果当前字符在当前节点的子元素中没有找到,那么就利用fail指针指向另外一个节点继续搜索,直到搜索完成,下图中的红线就是一个fail指针。
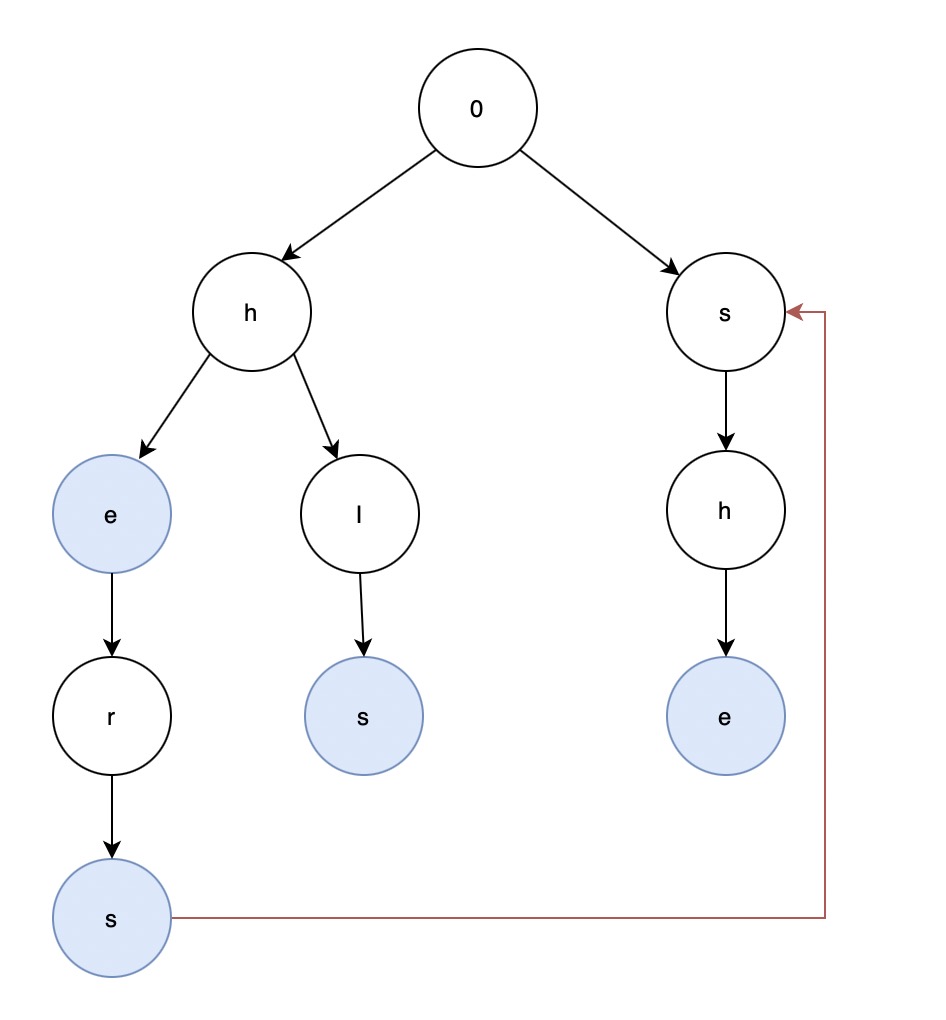
比如单词列表为['he', 'hers', 'his', 'she'],待分词文本为hershe,正常Trie匹配为先找到he,然后字符r再从0开始匹配,此时r没有在顶层节点的子节点当中,所以跳过,继续查找,直到找到了she完成。 而AC自动机的算法则为当找到了he单词后,继续在当前节点的子节点当中搜索字符r,如果有继续搜索下一个字符s,然后得到单词信息hers,然后继续搜索字符h,此时搜索位置为下图红色节点位置,但该节点下没有h:
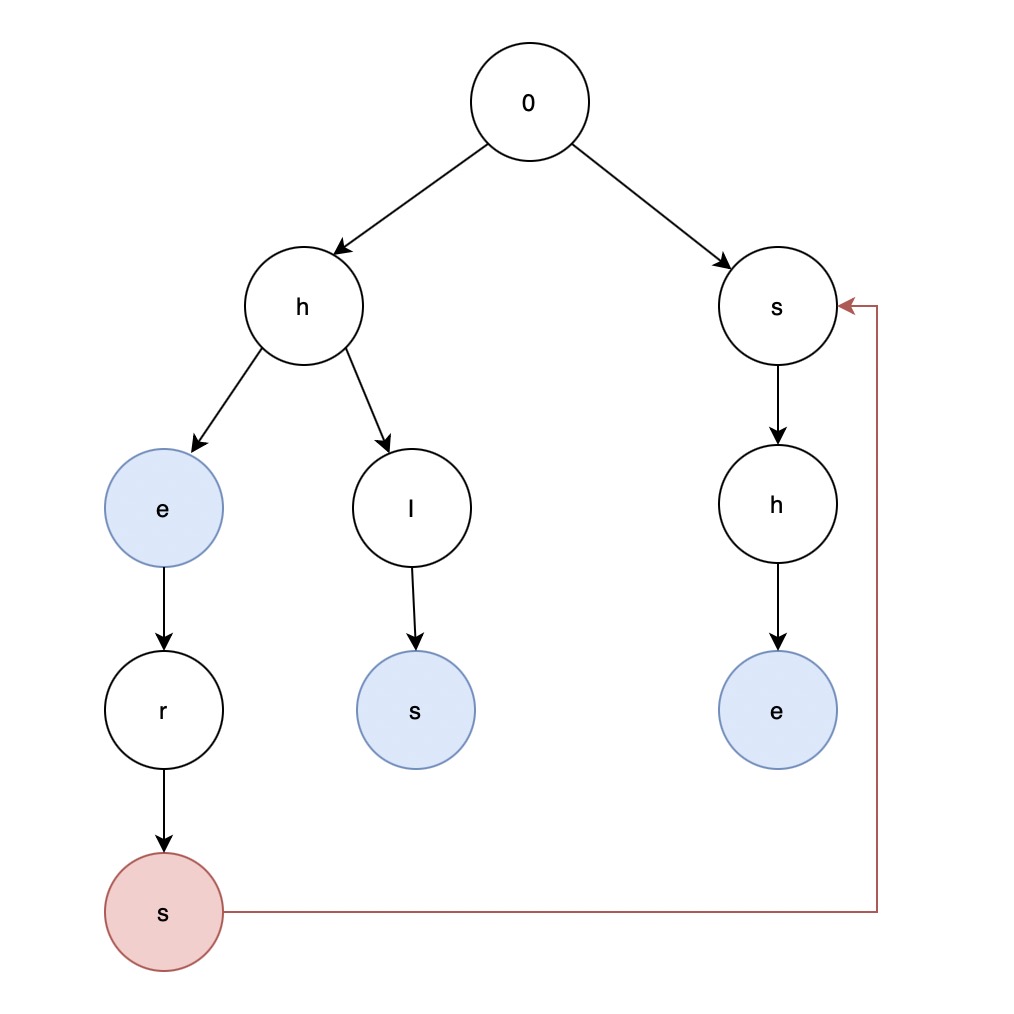
这个时候就查看当前节点(即红色节点)的fail指针(红线)指向的节点下是否有字符h,此时发现有,则通过fail指针继续查找,直到找到了单词she。 AC自动机的理念是比较好理解,而难点在于如何计算fail指针指向谁,计算fail指针可以通过BFS(层次遍历),BFS将Trie每一层进行遍历,遍历的时候将计算所有子节点的fail指针,并将子节点放入到一个先进先出容器当中(队列)便于访问子节点的子节点。 而计算fail指针的时候一定是当前字符不存在于当前节点的子节点当中,所以查找当前节点的子节点的fail指针的时候,可以通过将当前节点的子节点中的所有fail指针都可以获取到所有父节点的fail指针,然后一层一层的找,如果找到后就指向谁,如果没有找到则指向最顶层。 下面是实现的代码:
class TrieNode(object):
def __init__(self) -> None:
self._children = {}
self._fail = None
self._exist = []
def _add_child(self, char, value, overwrite = None):
child = self._children.get(char)
if child is None:
child = TrieNode()
self._children[char] = child
if overwrite:
child._exist.append(value)
return child
class Trie(TrieNode):
def __init__(self) -> None:
super().__init__()
def _find_text(self, text):
state = self
cut_word = []
for i,t in enumerate(text):
while state._children.get(t) is None and state._fail:
state = state._fail
if state._children.get(t) is None:
continue
state = state._children.get(t)
if len(state._exist) != 0:
for x in state._exist:
max_cut = text[i - x + 1:i + 1]
cut_word.append(max_cut)
return cut_word
def __setitem__(self, key, value):
state = self
for char in key:
if char == key[-1] :
state = state._add_child(char, len(value), True)
break
state = state._add_child(char, None, False)
def _init_fail(self):
q = queue.Queue()
for i in self._children:
state = self._children.get(i)
state._fail = self
q.put(state)
while q.empty() == False:
state = q.get()
for i in state._children:
v = state._children.get(i)
fafail = state._fail
while fafail is not None and fafail._children.get(i) is not None:
fafail = fafail._children.get(i)
v._fail = fafail
if v._fail:
if len(fafail._exist) != 0:
v._exist.extend(v._fail._exist)
q.put(v)